البعد الرابع – صادق علي القطري*

إن فكرة البعد الرابع ليست فكرة شخص واحد، وقد استدعى الأمر عددا من العقول المُبدعة لكي تتمكن هذه الفكرة من التأسيس والاندماج في الرياضيات. من بين الرواد، يمكن ذكر “لودويغ شلَيْفلي” و “ريمان الكبير**” والذي كانت لديه فكرة واضحة جدا حول البعد الرابع منذ منتصف القرن التاسع عشر.

لودويغ شلَيْفلي (1814-1895) هذا العقل الفذ يكاد اليوم يطويه النسيان، حتى من طرف علماء الرياضيات كان من أوائل العلماء الذين فطنوا إلى أنه وإن بدا فضاؤنا الطبيعي ثلاثي الأبعاد، فليس هناك ما يمنع من تصور فضاء “البعد الرابع”، وحتى من إثبات نظريات في الهندسة تخص كائنات رياضية من البعد الرابع. كان البعد الرابع، بالنسبة إليه، تجريدا صرفا؛ لكن ليس هناك أدنى شك في أنه وبعد سنوات من العمل، أصبح يشعر بارتياح أكثر في البعد الرابع عما كان عليه في البعد الثالث. كان عنوان مؤلَّفه الرئيس هو “نظرية الاستمرار المتعدد” (Theorie der vielfachen Kontinuität) وقد تم نشره سنة 1852***.

عادة ما يفكر الإنسان في أن أي فراغ له ثلاثة أبعاد: الطول والعرض والارتفاع. فالصندوق الذي طوله ستة أمتار، وعرضه أربعة أمتار، وارتفاعه متران، يمكن وصفه بمجموعة الأرقام (6,4,2). كما يمكن استخدام هذه المجموعة أيضًا لوصف ـ موقع نقطة في الفراغ ـ وليكن مثلاً موقع طائرة. غير أنه لا يمكن تحديد موقع طائرة متحركة بثلاثة أرقام. ولكي نستطيع تحديد موقع طائرة في الجو، بمجموعة الأرقام (6,4,2) مثلاً، فإننا نحتاج إلى بعد رابع هو الزمن.

يمكن لمسار الطائرة التي تطير في الجو أن يُحدَّد في أربعة أبعاد كما في الرسم البياني، وذلك عندما تقلع الطائرة من النقطة (0) وتطير نحو الجنوب الشرقي. فالموضع في المحور (س) يوضح مسافتها جنوب النقطة (0)، كما يوضح الموضع في المحور (ص) مسافتها شرق النقطة (0)، ويوضح الموضع في المحور (ع) ارتفاعها. أما المنحنى (ز) فإنه يمثل مسار الطائرة عبر الفضاء. وتحدد النقاط التي على المنحنى (ز) موضع الطائرة في أربعة أزمان مختلفة تسمى ز (0) إلى ز 4.

وفي أوائل القرن العشرين أدرك عالم الرياضيات هيرمان مِنكوفسكي أن النظرية النسبية التي أطلقها العالم الفيزيائي ألبرت أينشتاين وصفت كونًا ذا أربعة أبعاد. وكما يرى منكوفسكي فإن البعد الزمني يندمج مع الأبعاد المكانية الثلاثة ليشكل الزمان ـ المكان (الزمكان). بعد ذلك بدأ الرياضيون بدراسة أشكال هندسية ذات أربعة أبعاد أو أكثر. نحن نعرف أن في الكون ثلاثة أبعاد: البعد السيني, والبعد الصادي والبعد العيني. ولكن هل هناك أبعاد أكثر من هذه الثلاثة الأبعاد التي ألفناها؟ نحن نعرف أن المتجه إذا كان على صورة < س، ص > فهو متجه ثنائي أبعاد, وإذا كان على صورة < س، ص, ع > فهو متجه ثلاثي أبعاد. والمتجه < س، ص, ع > هو المتجه الذي بدايته نقطة الأصل (0,0,0) ونهايته النقطة (س, ص, ع). لكن ماذا لو عيًّنا متجها بالصورة < س, ص, ع, ط > وهل البعد ط موجود حقا؟ أم أن الكون مؤلف من ثلاثة أبعاد فقط؟ الجواب: نعم, هناك بعد رابع, ولنسميه ط. وهذا البعد قد يكون زماني وقد يكون مكاني.

إذا سلمنا أن البعد الرابع زماني, فإننا نستطيع أن نتخيل الوضع كأنه سلسلة أحداث أو فلم. فإن شكل الجسم في لحظة معينة قد يتغير في اللحظة التي تليها. وهذا البعد الذي تطرق إليه آينشتاين في نظريته النسبية وقد يكون البعد الرابع الذي نتحدث عنه بعدا مكانيا.

حتى في كنف مجتمع علماء الرياضيات، احتفظ البعد الرابع زمنا طويلا بمظهره الغامض والمستحيل. أما بالنسبة إلى عامة الناس فقد كان البعد الرابع يوحي تارة بقصص علم الخيال التي تجري فيها حوادث خارجة عن نطاق الحياة الطبيعية وتارة أخرى كان يوحي بالنظرية النسبية لآينشتاين: “البعد الرابع هو الزمن”.

والبُعد في الفيزياء والرياضيات يعرف لمكان أو لجسم بالحد الأدنى للإحداثيات اللازمة لتحديد أي نقطة في داخله. وهذه الخطوط لها بعدا واحدا لأن إحداثي واحد فقط هو المطلوب لتحديد النقطة عليه (على سبيل المثال، النقطة عند العدد 5 على خط الأعداد). للسطوح مثل المستوى أو سطح الأسطوانة أو الكرة لها بعدين لأنه لابد من وجود إحداثيين لتحديد نقطة عليه (على سبيل المثال، لتحديد موقع نقطة على سطح كرة نحتاج إلى خط العرض وخط الطول لتلك النقطة). داخل المكعب أو الأسطوانة أو الكرة فإن الأبعاد تكون ثلاثية لأن المطلوب ثلاث إحداثيات لتحديد نقطة ضمن هذا المكان. الرسم البياني التالي يبين من اليسار الى اليمين الانتقال من اللا بعد الى البعد الأول فما فوق:

 

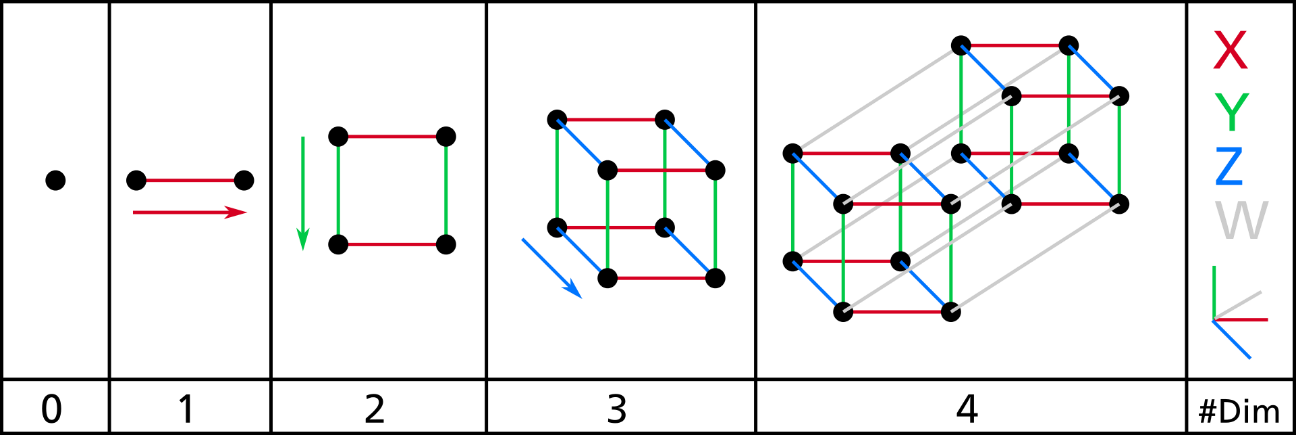
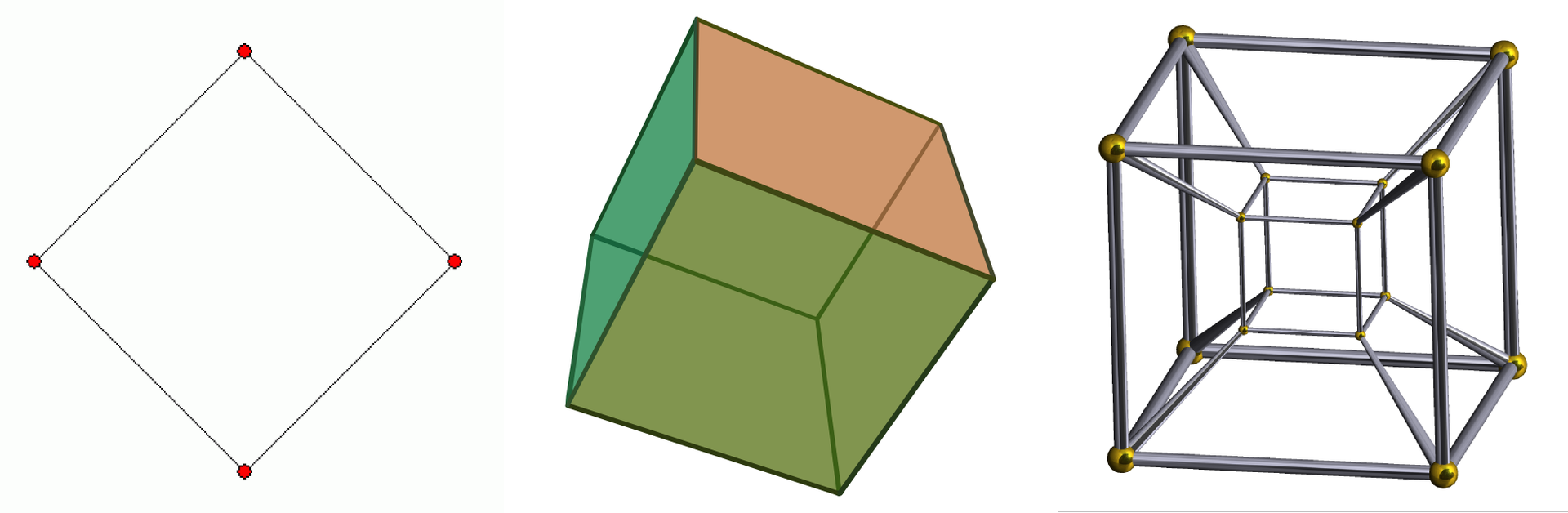
ولكي نتخيل البعد الرابع انظر الى الصورة المتحركة التالية:

كيف يمكن أن يكون الربع الرابع مكاني؟ كيف نتخيل الأجسام فيه؟

القطعة المستقيمة عبارة عن مجموعة نقاط مصفوفة على بعد واحد. والأجسام الثنائية الأبعاد كالمثلث والمربع والدائرة تتألف من مجموعة قطع مستقيمة وكل هذه الأجسام تعيش في عالم ثنائي الأبعاد وترى بعضها البعض كخطوط مستقيمة. فهي تألف البعد السيني والصادي وتبرمج عقلها على أن الكون مؤلف من بعدين فقط. وتستطيع التحرك يميناً ويساراً, وشمالاً وجنوباً. لكنها لا تستطيع أن تتحرك, ولا أن تتخيل, الاتجاه الأعلى والأسفل. فعندما تذهب للمدرسة ويشرح لها مدرس الهندسة الرياضية, وهو أيضا جسم ثنائي الأبعاد, عن المستقيمات والمتجهات والأجسام ذات البعدين < س، ص > فتألف المادة وتبدع فيها. لكن إذا وصلوا في مادة هندسة الرياضيات إلى المتجه ذي الثلاثة أبعاد < س, ص, ع > فإنه لا يستطيع أن يتخيله ولا يستطيع أن يراه, رغم كونه موجودا. ولا يسعه تخيل الأجسام ذات الثلاثة أبعاد مثل المكعبات والأهرام والكرات, ولا يستطيع أن يراها. والمكعبات والأهرام والكرات عبارة عن أجسام تتكون من عدة شرائح ثنائية الأبعاد.

وإذا زار الجسم الثلاثي الأبعاد العالم الثنائي الأبعاد, فإن الأجسام ثنائية الأبعاد لا تستطيع أن تراه ولا حتى أن تتخيله. وإذا مر جسم ثلاثي أبعاد واخترق المستوي الذي يعيشون فيه فإنهم فقط سيرون شريحة واحدة فقط من الشرائح المكونة له وهي انعكاس الجسم ثلاثي الأبعاد على العالم ثنائي الأبعاد وهذا الانعكاس ثنائي الأبعاد أيضا وتراه الأجسام الأخرى كخط مستقيم.

والشيء نفسه ينطبق علينا، نحن الأجسام المكونة من ثلاثة أبعاد ونألف الأبعاد الثلاثة السينية والصادية والعينية. ونرى انعكاسات الأجسام الثلاثية الأبعاد والتي هي ثنائية أبعاد. ولكننا لا نألف بعداً رابعاً. ولا نستطيع أن نتخيل الأجسام ذات الأربعة أبعاد ، لكننا نستطيع أن نرى انعكاسها على عالمنا الثلاثي الأبعاد. وكما أن العالم الثلاثي الأبعاد عبارة عن مجموعة عوالم ثنائية الأبعاد (مستويات) متراصة فوق بعضها البعض، فإن العالم الرباعي الأبعاد عبارة عن مجموعة عوالم ثلاثية الأبعاد فوق وجنب وخلف بعضها البعض. وهذه أشكال انعكاسات جسيم الرباعي الأبعاد في العالم ثلاثي الأبعاد.

و لتقريب الفكرة شاهد هذا المقطع (14:29 دقيقة):

الهوامش:
* إعداد واقتباس بتصرف
** ريمان الكبير: جورج فريدريك برنارد ريمان عالم رياضيات ألماني اشتهر بمساهمته في الهندسة التفاضلية ونظرية الأعداد والتحليل المعقّد. وقدم الأساس الرياضي للنظرية النسبية لألبرت أينشتاين. المصدر:https://www.arageek.com/bio/bernhard-riemann
*** https://mathshistory.st-andrews.ac.uk/Biographies/Schlafli

المراجع:

1. https://www.marefa.org/%D8%A7%D9%84%D8%A8%D8%B9%D8%AF_%D8%A7%D9%84%D8%B1%D8%A7%D8%A8%D8%B9
2. https://ar.wikipedia.org/w/index.php?title=%D8%A8%D8%B9%D8%AF&action=edit&section=1
3. https://www.youtube.com/watch?v=h6V_yZjWa8A
4. https://ar.wikipedia.org/wiki/%D9%81%D8%B6%D8%A7%D8%A1_%D8%B1%D8%A8%D8%A7%D8%B9%D9%8A_%D8%A7%D9%84%D8%A3%D8%A8%D8%B9%D8%A7%D8%AF#:~:text=%D8%A5%D8%B0%D8%A7%20%D8%B3%D9%84%D9%85%D9%86%D8%A7%20%D8%A8%D8%A3%D9%86%20%D8%A7%D9%84%D8%A8%D8%B9%D8%AF%20%D8%A7%D9%84%D8%B1%D8%A7%D8%A8%D8%B9,%D8%A7%D9%84%D8%B0%D9%8A%20%D9%86%D8%AA%D8%AD%D8%AF%D8%AB%20%D8%B9%D9%86%D9%87%20%D8%A8%D8%B9%D8%AF%D8%A7%D9%8B%20%D9%85%D9%83%D8%A7%D9%86%D9%8A%D8%A7%D9%8B.
5. https://ar.wikipedia.org/wiki/%D8%A8%D8%B9%D8%AF
6. http://www.dimensions-math.org/Dim_CH3_AR.htm