علوم القطيف مقالات علمية في شتى المجالات العلمية
الطريق الى نبع الوجود (12)
رحلة الحائرين إلى الله
قراءة في كتاب “وجود الله بين العلم و المنهج العلمي”
القسم الثاني
الكاتب : علي ديلان
بعد أن عرفنا الإحتمال فإنه من المفيد أن نذكر بعض القواعد المهمة في حساب الإحتمالات ثم نتطرق إلى بعض أقسام الإحتمال حيث ذكر الـ “ديلان” ثلاثة أنواع من الإحتمالات تتعلق بموضوع الكتاب.
قواعد الإحتمال
في ما يلي جملة من القواعد المهمة في حساب الإحتمالات. سألتزم بالعناوين كما وردت في كتاب الـ”ديلان” لكني سأعرض المادة على طريقتي:
- قاعدة الضرب
تجري قاعدة الضرب في الإحتمالات المستقلة و الإحتمالات المشروطة وذلك عند حساب القيمة الإحتمالية لحدثين أو أكثر. لنفترض أننا بإزاء حدثين (أ) و (ب) ، فإن كان الحدثين مستقلين ، فإن القيمة الإحتمالية للحادثتين هي حاصل ضرب القيمة الإحتمالية للحادثة (أ) في القيمة الإحتمالية للحادثة (ب):
ح (أ، ب) = ح (أ) . ح(ب)
حيث
ح(أ، ب) : احتمال الحادثتين أ و ب
ح(أ) : احتمال الحادثة أ
ح(ب): احتمال الحادثة ب
و بما أن الحادثتين مستقلتين فإن ح(ب ،أ) = ح (ب) . ح ( أ) = ح ( أ ، ب)
مثال: لنفترض أن سباقا يجري بين ثلاثة أحصنة أ ، ب و ج و أن القيم الإحتمالية لفوز الحصان أ و ب و ج على الترتيب هي
ح(أ) =1/2 ، ح( ب) = 1/3 ، ح (ج) =1/6
و لنفترض أننا أجرينا السباق بينهم مرتين ، فما هي الإحتمالات المختلفة لفوز أحدهما في السباقين ؟
من الواضح أن احتمال الفوز في السباق الثاني لا يتأثر باحتمال الفوز في السباق الأول و بالتالي فإن احتمالات الفوز المختلفة في السباقين:
ح( أ ، أ ) = ½ . ½ =1/4 ، ح( أ ، ب) = ½. 1/3 =1/6 ، ح ( أ ، ج ) = ½ . 1/6= 1/12
ح(ب،ب ) = 1/3. 1/3 =1/9 ، ح( ب ، أ ) = ح( أ ، ب) =1/6 ، ح ( ب ، ج) = 1/3 . 1/6 =1/18
ح(ج ، أ ) = ح(أ، ج)=1/12 ، ح( ج ،ب) = ح( ب ، ج)=1/18 ، ح(ج ، ج) = 1/6 . 1/6=1/36
أما إذا كان الحدثين (أ) و (ب) غير مستقلين حيث يكون احتمال الحادثة الثانية مشروطا أو متأثرا باحتمال الحادثة الأولى فإن القيمة الإحتمالية لهما تكتب على النحو التالي:
ح(أ، ب) = ح(أ) . ح(ب/ أ)
حيث أن
ح(ب/ أ): احتمال الحادثة ب على فرض وقوع الحادثة أ.
مثال: لنفترض أن لدينا 12 كرة ، خمسة منها حمراء و أربعة منها خضراء و ثلاثة منها صفراء. فما هو احتمال إستخراج ثلاثة كرات بصورة عشوائية على أن تكون كلها حمراء ؟
نحن أمام حالتان مختلفتان من القيم الإحتمالية:
الحالة الأولى: بعد عملية الإستخراج العشوائي للكرة من الوعاء في كل مرة يتم إعادتها للوعاء. ففي هذه الحالة يكون احتمال إستخراج كرة حمراء في المرة الثانية غير متأثر باحتمال إستخراجها في المرة الأولى ، كما أن احتمال إستخراج كرة حمراء في المرة الثالثة غير متأثر باحتمال سحبها في المرة الثانية. فنحن بإزاء حوادث مستقلة عن بعضها البعض و بالتالي فإن احتمال إستخراج ثلاثة كرات عشوائيا على أن تكون جميعها حمراء هو:
ح ( حمراء ، حمراء ، حمراء ) = 5 / 12 . 5/12 . 5/ 12 = 125/ 1728= 0.0723
الحالة الثانية: أن الكرة التي يتم استخراجها من الوعاء في كل مرة لا تعاد إلى الوعاء. ففي هذه الحالة يكون احتمال استخراج كرة حمراء للمرة الثانية يتأثر باحتمال استخراجها في المرة الاولى ، و احتمال إستخراجها في المرة الثالثة يتأثر باحتمال إستخراجها في المرة الثانية. و هذا النوع من الإحتمالات يسمى بالإحتمالات المشروطة. و بالتالي فإن احتمال استخراج كرة حمراء في المرة الأولى يساوي 5/12 ، و احتمال استخراج كرة حمراء في المرة الثانية يساوي 4/11 و احتمال استخراجها في المرة الثالثة يساوي 3/10. عندئذ تكون قيمة احتمال استخراج ثلاثة كرات عشوائيا على أن تكون جميعها حمراء هي:
ح( حمراء ، حمراء ، حمراء ) = 5/12 . 4/11 . 3/10 = 125/1320 = 0.0455.
- قاعدة الجمع
تجري هذه القاعدة في حساب القيمة الإحتمالية لمجموعة الحوادث المنفصلة. فلو كان لدينا حدثين (أ ) و (ب) منفصلين و طلب منا حساب القيمة الإحتمالية لهما فإن احتمال و قوع أحدهما هو عبارة عن مجموع احتمال (ا) مع احتمال (ب) و تكتب بالصيغة التالية:
ح ( أ U ب) =ح(أ) + ح(ب)
حيث ح ( أ U ب) تعني احتمال وقوع أ أو ب. و يطلق على هذا النوع من الإحتمال بالإحتمالات المتنافية لأن الحادثتين لا يمكن لهما أن يجتمعا فوقوع أحدهما يمنع وقوع الأخرى. فمثلا لو رمينا قطعة نرد لمرة واحدة فإن حدث ظهور عدد زوجي ( 2,4,6) يتنافى مع حدث ظهور عدد فردي ( 1,3,5) ، فإن أحد الحدثين لابد له أن يقع.
مثال: سحبت بطاقة عشوائيا من مجموعة 20 بطاقة مرقمة من 1 إلى 20. فما احتمال الحصول على عدد يقبل القسمة على 5 أو عدد يقبل القسمة على 7؟
الأعداد التي تقبل القسمة على 5 هي: ( 5, 10, 15 ,20 ) ، أما الأعداد التي تقبل القسمة على 7 هي : ( 7, 14). و بما أن لا يوجد شيء مشترك بينهما فإن الحدثين متنافين و يكون احتمال أحدهما يساوي ( 4/20 + 2/20 =6/20).
أما إذا كان لدينا مجموعة من الحوادث بحيث يكون وقوع أحدها لا يمنع من وقوع الأخرى فإن هذه الحوادث متداخلة و يطلق على هذا النوع ىمن الإحتمال بالإحتمالات الغير متنافية. فلو كان لدينا حدثين (ا) و (ب) غير متنافيان فإن احتمال وقوع أ أو ب تصاغ على الشكل التالي:
ح (أ U ب) = ح(ا) +ح(ب) –ح(أ ب)
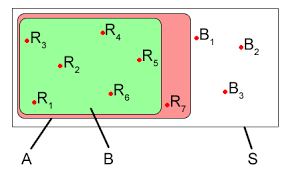
حيث أن ح(أ ب) تعني القيمة الإحتمالية للقدر المشترك بينهما. فعند رمي قطعة من النرد لمرة واحدة فإن حدث ظهور عدد زوجي (2,4,6) لا يتنافى مع حدث ظهور عدد أقل من ثلاثة (1,2) ، فإن العدد 2 هو القدر المشترك بين الحادثتين. فيكون احتمال ظهور عدد زوجي أو عدد أقل من ثلاثة عبارة عن ( 3/6+2/6-1/6)=4/6. و لتوضيح هه القاعدة أكثر سأضرب مثالا آخر.
مثال: لنفترض أن طالبا قد أختير عشوائيا من بين 80 طالبا ، ثلاثون منهم يدرسون الرياضيات و عشرون منهم يدرسون الكيمياء و عشرة منهم يدرسون الرياضيات و الكيمياء. فما احتمال أن يقع الإختيار على طالب يدرس الرياضيات أو الكيمياء؟ فقد يقع الإختيار العشوائي على طالب يدرس الإثنين معا. و بالتالي فإن:
ح ( الرياضيات U الكيمياء ) = ح(الرياضيات) + ح( الكيمياء) –ح( الرياضيات الكيمياء)= 30/80 – 20/80- 10/80= ½.
- علاقة بايس “مبدأ الإحتمال العكسي”
تجري هذه القاعدة التي تعرف بإسم مكتشفها البريطاني توماس بايس في القرن الثامن عشر في الإحتمالات المشروطة. و مفاد هذه القاعدة هو أن احتمال الحدث ( أ) بشرط وقوع حدث آخر (ب ) يعطى بالصيغة التالية :
ح(أ | ب) = حيث أن
ح(أ | ب) تعني احتمال و قوع الحدث أ بشرط وقوع الحدث ب. و ح( ب|أ) احتمال ب على شرط وقوع أ .
مثال: لنفترض أن سكن طلاب في كلية يتكون من:
- 30% طلاب سنة أولى و 10% منهم يمتلكون سيارة ،
- 40 % طلاب سنة ثانية و 20 % منهم يمتلكون سيارة ،
- 20% طلاب سنة ثالثة و 40% منهم يمتلكون سيارة ،
- 10% طلاب سنة رابعة و 60% منهم يمتلكون سيارة . فإذا اخترنا طالبا يمتلك سيارة ، فما احتمال كون هذا الطالب في السنة الثالثة ، ح ( ج|هـ)؟
لنفترض أن أ ، ب، ج ، د تمثل على الترتيب مجموعة طلاب السنة الأولى ن الثانية ، الثالثة ، الرابعة . و لنفترض أن هـ تمثل مجموعة الطلاب الذين يمتلكون سيارة.
لنحسب أولا احتمال أن يكون الطالب يمتلك سيارة ، ح (هـ).
ح(هـ)= ح(أ)ح(هـ|أ)+ح(ب)ح(هـ|ب)+ح(ج)ح(هـ|ج)+ح(د)ح(هـ|د)
=0.30 0.10 + 0.40× 0.20 + 0.20 × 0.40 + 0.10× 0.60 = 0.25
ح(ج|هـ)= ح(ج) . ح( هـ|ج)/ ح(هـ) =( 0.20 × 0.40) / 0.25 = 0.32
مثال: ثلاث الآلات أ ، ب و ج تنتج على الترتيب 40% ، 10% و 50% من المواد في مصنع. النسبة المئوية للمواد التي تنتجها هذه الآلات والتي بها عيوب على الترتيب 2%، 3% و 4%. فإذا ما أختيرت مادة عشوائيا و كانت هذه المادة معطوبة ، فما هو احتمال أن تكون الآلة التي انتجتها هي الآلة أ ؟
باستخدام قانون بايس:
لنفترض أن د ترمز للمادة المعطوبة فإن احتمال أن تكون الآلة أ هي المسؤولة عن إنتاجها هو
ح(أ|د) = ح(أ).ح(د|أ)/ ح(د)
حيث ح(د) يمثل احتمال كون الآلة معطوبة
ح(د) = ح(أ) ح(د|أ)+ح(ب) ح(د|ب)+ح(ج) ح(د|ج)= 0.40 × 0.02 + 0.10 × 0.03 + 0.50 × 0.04=0.031
ح(أ|د)=( 0.40 ×0.02)/0.031=0.258= 25.8 %
قانون برنولي “نظرية التوزيع”
يستخدم قانون برنولي أو ما يعرف بنظرية التوزيع في الحالات التي نود فيها معرفة القيمة الإحتمالية لوقوع حادثة معينة عدد م من المرات ضمن مجموعة ، ن ، من الإختبارات العشوائية ذات الناتجين فشل أو نجاح. و نحتاج في استخدام هذا القانون إلى معرفتنا المسبقة بالقيمة الإحتمالية القبلية للحادثة أي احتمال النجاح في هذه الإختبارات. و لنرمز لإحتمال النجاح في هذه الإختبارات بـ ر، و احتمال الفشل بـ ل ، حيث ل =(1-ر) فإن قانون برنولي يصاغ على النحو التالي:
ح(م) = رم لن-م= رم لن-م
حيث ح(م) تمثل احتمال ظهور الحادثة م من المرات.
و ن! /(ن-م)! م! هي القاعدة المعروفة بالتوافيق.
مثال: لنفترض أننا رمينا قطعة من النقود ستة مرات فما احتمال ظهور وجه الصورة مرتين؟
من المعروف ان احتمال ظهور وجه الصورة (احتمال النجاح)، ر=½ و احتمال الفشل اي ظهور وجه الكتابة هو ل= (1-1/2)=½ و باستخدام قانون برنولي يمكن أن نعرف احتمال ظهور وجه الصورة مرتين.
ح(2) = 26-2= 0.234= 23.4%
مثال: لو أطلقنا سهما باتجاه هدف سبع مرات و كان احتمال إصابة الهدف 1/3 و بالتالي فإن احتمال الفشل هو 2/3. فما هو احتمال أن يصيب السهم الهدف ثلاثة مرات؟
ح(3) = 34 = 0.26=26%
بعد أن استعرضنا بعض القواعد المهمة في حساب الإحتمالات ، نعود لنذكر بعض أقسام الإحتمالات و التي ذكر منها الـ”ديلان” ثلاثة أقسام.…………قريبا الطريق الى نبع الوجود (13).